Anthony Maggs, CNRS, ESPCI, PSL

Mail: Tony Maggs, ESPCI Paris, PSL Research University, 10 Rue Vauquelin, 75005, Paris, France.
E-mail:
ORCID HAL arXiv
Link between the true self-avoiding walk and event driven simulation
code on GitHub

General potentials
Smoluchowski aggregation with worms
Effective interactions and non-central forces in hard sphere crystals
>
Cavity averages for hard spheres in the presence of polydispersity and incomplete data
How many modes can be studied in colloids by correlation analysis?
Crystallization and sedimentation in colloids
with John Russo , Hajime Tanaka , Daniel Bonn
Mode structure from truncated correlations
Truncated correlations in video microscopy of colloidal solids
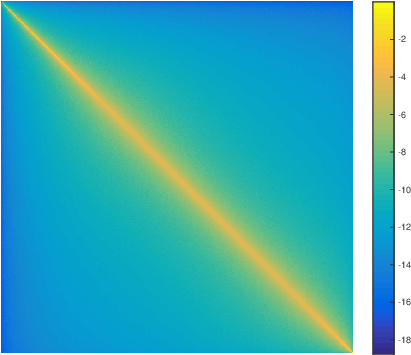
Use of integral equations such as \[ \int_V \frac{1}{4\pi|{\bf r}-{\bf r'}|} \psi({\bf r}) \; d^3{\bf r} = \Lambda \psi({\bf r'}) \] to understand experimental mode structure in a fluctuating elastic medium
Study of two-dimensional colloid with experimental and theoretical groups of U. Penn.
Anomalous dispersion in sliced colloids

Why does a colloid have the anomalous dispersion law $\omega^2 =q $ when observed in a confocal slice? The density of states then behaves as $\rho(\omega) \sim \omega^3$
Anisotropic elasticity and confocal microscopy
Elastic constants from confocal microscopy with Claire Lemarchand, Michael Schindler thesis in French
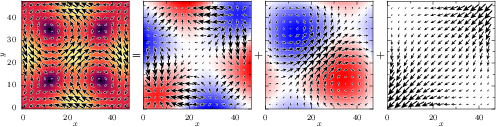
Fluctuations and modes in a colloidal crystal with Daniel Bonn, Antina Ghosh,

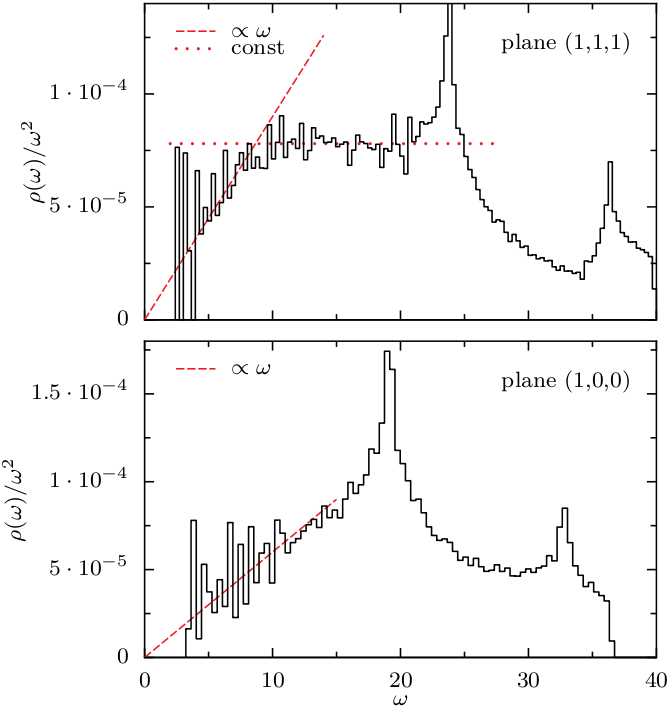Density of states in two cuts of a colloidal crystal.

Casimir, Lifshitz and dielectric fluctuations
Dynamic Casimir with David Dean , Bing-Sui Lu and Rudi Podgnornik
Influence of scale dependent dieletric constant on interactions
Application to Monte Carlo in fluids with Helene Berthoumieux Showing how to go beyond approximations such as Axelrod-Teller.
Lifshitz in two and three dimensions
Evaluation of dispersion forces in general geometries with Samuela Pasquali
Thermal Casimir/Lifshitz interactions- discretization methods
Generation of thermal Casimir in Monte Carlo
The transliteration of Лифшиц can also be Lifschitz or Lifshits
Two disks for which the full electrodynamic interaction is found by evaluating a functional determinant $$F=\int_0^\infty \log ( {\det{[{\mathcal D} (\omega)])}}\frac{ d\omega}{2\pi}$$

Quantum spins and Computing
Quantum annealing appears to give a simple means of finding the solution to difficult problems, however a first order phase transition can lead to exponential slow-downs
Quantum annealing with Florent Krzakala and Jorge Kurchan
Quantum optimization
Quantum energy gaps with Justine Pujos
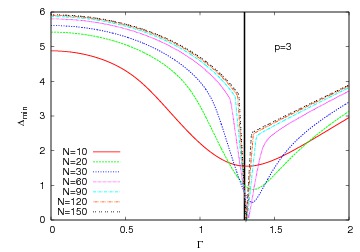Evolution of the gap in a quantum system as a function of coupling for various systems sizes

Multi-scale Monte Carlo algorithm for Lennard-Jones fluids
Introduce a collective update in a fluid which moves many particles simultaneously. It leads to simultaneous equilibration on all length scales, but requires the determinant of the transformation as a correction in the Metropolis update rule.
Multi-scale Monte Carlo for Lennard-Jones fluids
Virial theorem
Leapfrog algorithm with a conserved quasi-energy
Multi-scale molecular dynamics
Approximation-free simulation with event-chain methods

Equation of state of soft disks with Yoshihiko NISHIKAWA
Hard-disk computer simulations, historic perspective
Sparse Hard-Disk Packings and local Markov Chains
Large scale dynamics of ECMC
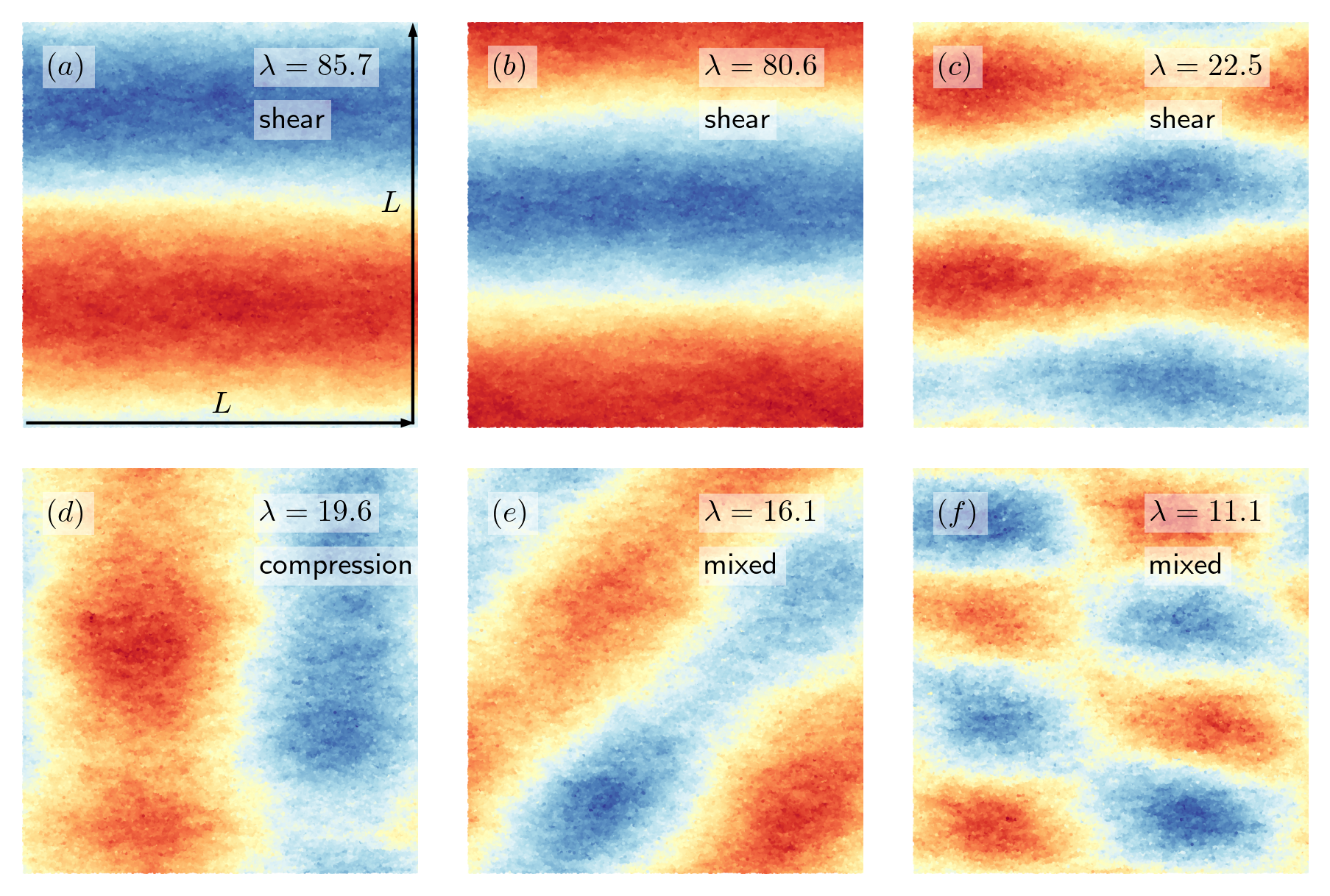
event-chain Monte Carlo with local times
Event Chain Monte Carlo with Michael Faulkner, Liang Qin, Werner Krauth
JellyFysh documentation with Philipp Hoellmer
Factor field acceleration with Ze Lei and Werner Krauth

Local electrostatics in molecular dynamics and Monte Carlo
Convex Poisson-Boltzmann equations beyond mean field
disjoining pressure isotherm in non-symmetric conditions
Density gradiants and Poisson-Boltzmann
Asymmetric excludedvolume in electrolytes
Fluctuations and spectrum in dual Poisson-Boltzmann theory
Kirkwood-Shumaker interactions in one dimension with Rudi Podgornik
Fluctuations beyond Poisson Boltzmann theory with Zhenli Xu
Convex functional for Poisson-Boltzmann theory of ionic solutions using Legendre transforms to produce dual variational principles
Legendre transforms in electostatics with Justine Pujos
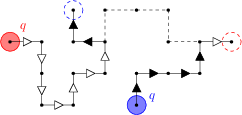
We can use the constraint of Gauss' law: $ \; div\;{\bf E} - \rho =0 $ to produce, local $O(N)$ Monte Carlo algorithms for the simulation of charged systems
Summary of Local electrostatics
Metallic and 2+1 dimensional boundary conditions with Lucas Levrel link to Thesis in French
Simulating nanoscale dielectric response with Ralf Everaers
Discretization artefacts, higher order corrections in electrostatic interpolation
Mobility and trail dynamics
Comparison of molecular dynamics and Monte Carlo for CCP2004
Cluster algorithms for Statphys22 with Fabien Alet
Molecular dynamics, with Joerg Rottler
Off-lattice Monte Carlo, with Joerg Rottler
Auxiliary field Monte Carlo for charged particles, inhomogeneous media and Poisson-Boltzmann
An algorithm for local Coulomb simulation, for a simple lattice gas with Vincent Rossetto link to thesis in French
Relaxation dynamics of a local Coulomb
Ewald summation unpublished notes on simple optimizations for Monte Carlo
Polarized multiple scattering
The theory of polarization in multiple scattering is very similar to the theory of writhe in semiflexible polymers, such as DNA:
Writhing Light in multiple scattering
Polarization patterns in back scattering
Berry Phases and multiple scattering
Flower-like figure from observation of polarized light in strongly scattering sample. Four-fold symmetry from the Berry phase of $4 \pi$ in backscattering geometry.
Writhe geometry
Formulations of the writhe based on the local torsion, $\tau$ can not be used in polymer physics, one must use more global considerations to understand the geometry
Writhing geometry of open DNA
Comment on DNA elasticity
Geometry of writhe
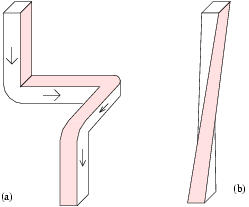
A bent beam with writhe leads to rotation.
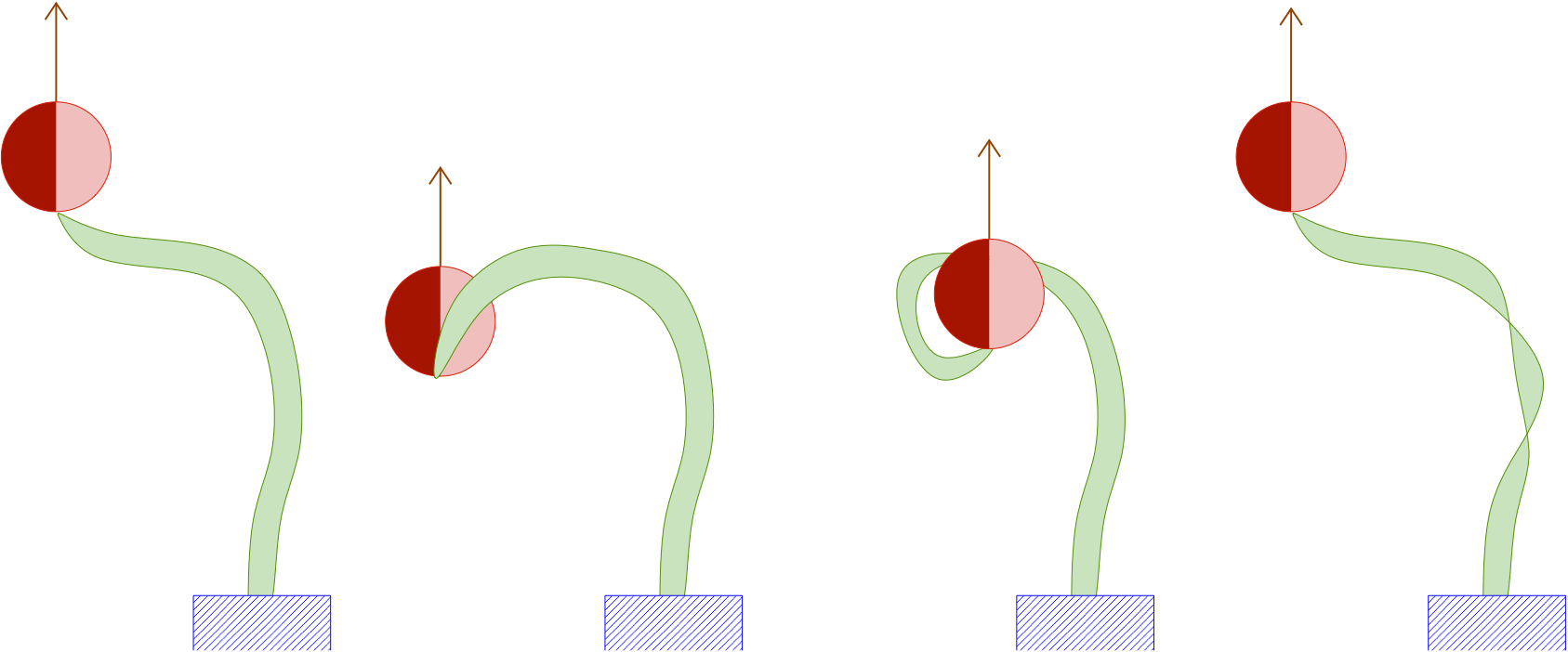
Writhe is only defined modulo $ 4 \pi $ in open geometries
Semiflexible polymers
Anisotropic dynamics in semiflexible polymers leads to a mixture of transverse dynamics in $ t^{3/4} $ and longitudinal dynamics in $ t^{7/8} $.
Anisotropic fluctuations
Two plateau moduli for actin gels
Sub-diffusion and anomalous
Non-affine effects in micro-rheology
Actin filaments have a persistence length of $10\mu$, this is much stiffer than most polymers. How does this affect the rheology and mechanics of semi-diluate solutions? The modulus is given by $G= \frac{kT}{\ell_e}$ where the collision length in the tube $\ell_e$ is close to a micron. Uncrosslinked actin is thus rather soft.
Dynamics and rheology of actin solutions Hervé Isambert
unbinding stiff polymers
Microtubule motor constructs
Concentration of motors in microtubule arrays with Francois Nedelec
Regulation of microtubule growth Marileen Dogterom
Organization of microtubules by motors Thomas Surrey

Long range interactions in metallic systems
In a classical plasma one normally expects that correlations are short ranged -- due to Debye screening. In quantum mechanics the situation is more complicated we show here how long-ranged interaction are generated in an electron plasma in a way that is reminiscent of van der Waals interaction in $1/r^6 $
Absence of screening in the quantum Coulomb system with Neil Ashcroft
Polymer Flow
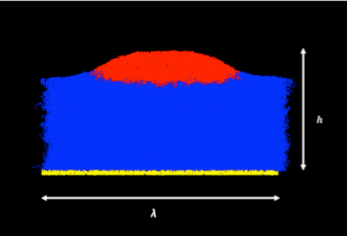
Viscocapillary leveling
Colloidal fluctuations

Simulations of self assembling fluid membranes
Can one build a model of locally interacting particles which self assemble into a fluctuating fluid membrane
Fluid membranes